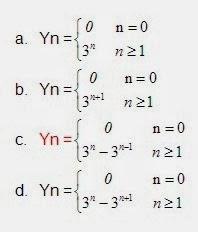MATIF : FUNGSI NUMERIK

FUNGSI NUMERIK

Fungsi Diskret Numerik (disingkat fungsi numerik) adalah fungsi yang domainnya Bilangan bulat nonnegatif, dan kodomainnya bilangan real. Sebuah fungsi adalah sebuah relasi biner yang secara unik menugaskan kepadasetiap anggota domain, satu dan hanya satu elemen kodomain. Fungsi diskrit numerik,atau singkatnya disebut fungsi numerik, adalah sebuah fungsi dengan himpunanbilangan cacah sebagai domain dan himpunan bilangan riil sebagai kodomainnya.Fungsi numerik ini menjadi pokok bahasan yang Menarik karena sering digunakandalam komputasi digital.

MANIPULASI FUNGSI NUMERIK

Jumlah dari dua fungsi numerik adalah sebuah fungsi numerik yang harganya pada n tertentu sama dengan jumlah harga-harga dari kedua fungsi numerik pada  n.

Contoh 4.1.

Jika diketahui   a_n = 2ⁿ , n ³ 0,    b_n = 5 , n ³ 0    dan    c_n = a_n + b_n  ,

maka  c_n = 2ⁿ + 5 , n ³ 0.                                                                                                          ð

Hasil kali (produk) dari dua fungsi numerik adalah sebuah fungsi numerik yang harganya pada  n  tertentu sama dengan hasil kali harga-harga dari kedua fungsi numerik pada  n.

Contoh 4.2.

Jika diketahui   a_n = 2ⁿ , n ³ 0,    b_n = 5 , n ³ 0    dan    d_n = a_n . b_n  ,

maka   d_n = 5(2ⁿ) , n ³ 0.

Beda maju (forward difference) dari sebuah fungsi numerik  a_n  adalah sebuah fungsi numerik yang dinyatakan dengan   Da , dimana harga  Da  pada n sama dengan harga    a_n+1 - a_n .

Da = a_n+1 - a_n  ,   n ³ 0.

Beda ke belakang (backward difference) dari sebuah fungsi numerik  a_n  adalah sebuah fungsi numerik dinyatakan dengan Ña , dimana harga Ña pada n = 0  sama dengan harga a₀  dan  harga  Ña  pada n ³ 1 sama dengan  a_n - a_n-1 .

Ña  =  .

Contoh 4.3.

Misalkan  b_n = 9ⁿ , n ³ 0  dan    e_n = Db,  maka     e_n = 9ⁿ ,  n ³ 0                                        

Contoh 4.4.

Misalkan  b_n = 9ⁿ , n ³ 0  dan    f_n = Ñb,  maka   

                                                         

  f_n =      

SOAL FUNGSI NUMERIK !!!!

1.    Jika diketahui Yn = 3ⁿ dan Zn = 4 untuk n ≥ 0 dan Xn = Yn + Zn, maka ....

a.    Xn = 4ⁿ + 3          

b.    Xn = 3ⁿ = 4

c.    Xn = 3ⁿ + 4

d.    Xn = 3 + 4n

JAWAB :

Jumlah dari dua fungsi numerik adalah sebuah fungsi numerik yang harganya pada n tertentu sama dengan jumlah harga-harga dari kedua fungsi numerik pada n. Jika Yn = 3ⁿ dan Zn = 4 dan Xn = Yn + Zn maka Xn = 3ⁿ + 4 ...... C. Xn = 3ⁿ + 4

2.    Jika diketahui Yn = 5ⁿ dan Zn = 3 untuk n ≥ 0 dan Xn = Yn . Zn, maka ....

a.    Xn = 5ⁿ3ⁿ

b.    Xn = 3(5ⁿ)

c.    Xn = (5ⁿ)³

d.    Xn = 5ⁿ/3

JAWAB :

Hasil kali dari dua fungsi numerik adalah sebuah fungsi numerik yang harganya pada n tertentu sama dengan hasil kali harga-harga dari kedua fungsi numerik pada n.Jika Yn = 5ⁿ dan Zn = 3 dan Xn = Yn . Zn maka Xn = 3(5ⁿ) .....B. Xn = 3(5ⁿ)

JAWAB :

Misalkan An adalah sebuah fungsi numerik dan i adalah sebuah integer positif. Kita gunakan SⁱA untuk menyatakan fungsi numerik yang nilainya 0 pada n = 0,1,…, (i-1) dan nilainya sama dengan A n-i pada n ≥ i. Dengan rumus :

   

4.     Jika Xn = 4ⁿ dan Yn = S^-3 untuk n ≥ 0, maka...

a.    Yn = 4ⁿ⁺³

b.    Yn = 4³

c.    Yn = 4^n-3

d.    Yn = 4³ⁿ

JAWAb :

Misalkan An adalah sebuah fungsi numerik dan i adalah sebuah integer positif. Kita gunakan S^-iA untuk menyatakan fungsi numerik yang nilainya sama dengan A n+i pada n ≥ 0.Dengan rumus :

S^-iA = A n+i

Jika Xn = 4ⁿ dan Yn = S^-3 maka Yn = 4ⁿ⁺³   ...... A. Yn = 4ⁿ⁺³

5.    Jika An = 5ⁿ dan Bn = ΔA untuk n ≥ 0,maka....

a.    Bn = 5ⁿ – n

b.    Bn = 5^n-1

c.    Bn = 5ⁿ⁺¹ – 5ⁿ

d.    Bn = 5ⁿ⁺¹ + 5ⁿ

JAWAB :

ΔA adalah beda maju dari An. Beda maju (forward difference) dari sebuah fungsi numerik An adalah sebuah fungsi numerik yang dinyatakan dengan ΔA , dimana harga ΔA pada n sama dengan harga An+1 - An sehingga jika An = 5ⁿ dan Bn = ΔA maka Bn = 5ⁿ⁺¹ – 5ⁿ  ..... C. 5ⁿ⁺¹ – 5ⁿ

6. .    Jika Xn = 3ⁿ dan Yn = ∇X untuk n ≥ 0,maka....

JAWAB :

Beda ke belakang (backward difference) dari sebuah fungsi numerik Xn adalah sebuah fungsi numerik dinyatakan dengan ∇X , dimana harga ∇X pada n = 0 sama dengan harga X0 dan harga ∇X pada n ≥ 1 sama dengan Xn - Xn-1 dengan rumus :

Jawab :

Jumlah dari dua fungsi numerik adalah sebuah fungsi numerik yang harganya pada n tertentu sama dengan jumlah harga-harga dari kedua fungsi numerik pada n.    

a. t_n = 

Jawaban :

9.    Jika bn = 2n , n ≥ 0 dan fn = ∇b, tentukan  fn =……..

JAWAB  :

Beda ke belakang (backward difference) dari sebuah fungsi numerik Xn adalah sebuah fungsi numerik dinyatakan dengan ∇X , dimana harga ∇X pada n = 0 sama dengan harga X0 dan harga ∇X pada n ≥ 1 sama dengan Xn - Xn-1 dengan rumus :

10. Jika bn = 2ⁿ , n ≥ 0 dan en = Δb, tentukan  maka en= …!!

a.    e_n = 2ⁿ, n ≥ 0

b.    e_n=2_n+1-2_n , n ≥ 0

c.    e_n=2_n-1+2_n , n ≥ 0

d.    e_n=n², n ≥ 0

JAWAB :

ΔA adalah beda maju dari bn. Beda maju (forward difference) dari sebuah fungsi numerikbn adalah sebuah fungsi numerik yang dinyatakan dengan ΔA , dimana harga ΔA pada n sama dengan harga A_n+1 - A_n sehingga jika bn = 2ⁿ dan en = ΔA maka  a. en = 2ⁿ, n ≥ 0.